*본 내용은 북두출판사에서 출간된 모터제어 제4판을 기반하여 작성되었습니다.
일반적으로 유도기라고 하면 교류 전류를 인가해서 동작하는 모터를 말한다. 교류 전동기라고도 명명할 수 있다.
고정자 3상 권선에 교류 전류를 흘려 생성된 회전자계와 회전자 전자석과의 상호작용에 의해 토크가 발생, 회전하는 원리를 갖는다.
간략히 구조적인 특징을 설명하자면, 고정자에 권선이 감겨있으며, 교류 전원은 3상 고정자 권선에만 공급된다. 이때 고정자 권선은 직류 전동기의 전기자 권선과 계자 권선의 역할을 동시에 수행한다.
회전자는 권선의 형식에 따라 농형과 권선형으로 나눌 수 있다.
농형 권선은 회전자 표면에 슬롯을 파서 도체 바를 나란히 넣어 양단이 단락되도록 구조를 갖는다. 이때 양쪽 끝을 단락시키기 위해 단락환(End ring)이라는 구조를 넣는다.
반면, 권선형 회전자는 고정자 권선과 같은 형태를 가지면서 회전자 권선의 끝부분을 3개의 슬립 링과 연결, 외부 회로와 연결되도록 구성된다. 회전자 권선은 보통 Y-결선으로 되어 있는데, 단자를 슬립링(slip ring)에 연결하여 브러시(brush)를 통해 외부 회로와 연결된다.


5.2 회전 자계(Rotating Magnetic Field)
본 장에서 소개하는 3상 유도기의 권선에서 흐르는 전류에 의해 발생하는 자계에 대한 고찰이 필요하다. 일반적으로 3상 전류가 흐를 때 각 전류의 위상은 120도의 차이를 갖는다. 이때 3상 유도기의 3상 권선은 고정자 내부 표면 공간에서 서로 전기적으로 120도씩 떨어져 설치된다. 이제 전류가 각 상권선에 흐르게 되면, 정현파 전류와 권선에 의해 정현파 기자력이 발생한다(자기 회로). 그리고 각 상별로 만들어진 기자력이 합성되면서 회전하는 형태의 자기장을 형성하게 된다. 이 합성 기자력은 권선에 흐르는 전류의 각속도로 공극에서 회전하므로 회전자계라 부른다.
회전자계 수식을 이해하기 위해 고정자 3상 권선에 흐르는 3상 전류에 의해 발생되는 합성 기자력을 구한다.
고정자 권선에 Im의 크기를 갖는 3상 평형 전류가 흐른다고 가정하면 각 상별 전류 수식은 아래와 같다.


$$ i_{a}=I_{m}cos\omega _{s}t$$
$$ i_{b}=I_{m}cos\left(\omega _{s}-120^{\circ}\right)$$
$$ i_{c}=I_{m}cos\left(\omega _{s}+120^{\circ}\right)$$
여기서 ws는 전류의 각속도이다.
수식적인 계산을 시작하기 전, 유도 전동기에서 3상 고정자 전류가 흐를 때 합성 기자력이 어떤 움직임을 갖는지 고려해보자.
시간이 지남에 따라 권선 전류 분포에 의한 기자력은 a상 → b상 → c상 권선 측 방향으로 움직이는 것을 알 수 있으며, 한 주기 변동에 대해 기계적으로 1회전을 한다.
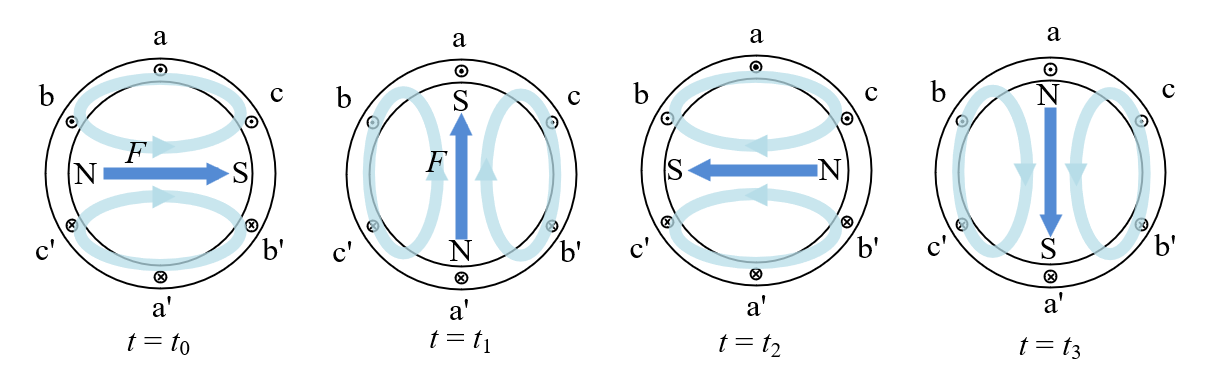
전기각 theta(2/P)= 기계각 theta_m이 된다.
$$\theta _{m}=\left(\frac{2}{P}\right)\theta $$
P극기에서 회전자계의 분당 속도(Revolution Per Minute, r/min)은 아래와 같이 도출된다.
$$n=\frac{2}{P}\cdot f_{s}\cdot 60=\frac{120f_{s}}{P}[\textrm{r/min}]$$
이제 3상 합성 기자력을 수식적으로 구해본다. 기자력은 권선 수와 전류의 곱으로 도출되며, 전류가 정현파로 흐르기 때문에 기자력 또한 시간에 따라 정현파적인 움직임을 보인다.
$$F_{a}\left(\theta\right)=N_{s}i_{a}cos\theta $$
$$F_{b}\left(\theta\right)=N_{s}i_{a}cos\left(\theta-120^{\circ}\right)$$
$$F_{c}\left(\theta\right)=N_{s}i_{a}cos\left(\theta+120^{\circ}\right)$$
이제 합성 기자력을 구하기 위해 각 상별 발생하는 기자력을 모두 더한다.
$$F\left(\theta\right)=F_{a}\left(\theta\right)+F_{b}\left(\theta\right)+F_{c}\left(\theta\right)=N_{s}I_{m}[cos\omega _{s}cos\theta+cos(\omega _{s}t-120^{\circ})cos(\theta-120^{\circ})+cos(\omega _{s}t+120^{\circ})cos(\theta+120^{\circ})]=\frac{3}{2}N_{s}I_{m}cos(\omega _{s}t-\theta)$$
위 식을 통해 우리는 3상 평형 전류에 의한 합성 기자력이 항상 일정한 크기를 갖고 공간상에 정현적으로 분포되며, 시간에 따라 전류의 각속도로 움직인다는 것을 알 수 있다.
'[전공]' 카테고리의 다른 글
| [전기기기공학] 05. 유도기(3) (0) | 2025.04.19 |
|---|---|
| [전기기기공학] 05. 유도기(2) (0) | 2025.04.17 |
| [전기기기공학] 02. 변압기(3) (0) | 2025.02.22 |
| [전기기기공학] 02. 변압기 (2) (0) | 2025.02.19 |
| [전기기기공학] 02. 변압기 (1) (0) | 2025.02.11 |



